[#13] Experiencing Theory: The Gate To Understanding

[#13]  Experiencing Theory: The Gate To Understanding

By Piet Hut

Science is based on theory and experiment.  We may think that theorists work with their minds, in an abstract way, while experimenters work with their hands, directly experiencing the world of matter and measurements.  We talk about an experienced builder, or user, of experimental equipment.  But to become a good theorist, presumably you would also need to become experienced.  What would it mean to experience a mathematical equation?

“thought experiments”

As a hint, it is interesting to consider that physicists often talk about thought experiments.  Einstein was famous for deriving his theory of relativity, in its various forms, by first conducting imaginary experiments.  For example, he imagined floating in an elevator without windows, realizing that he could not discriminate between the elevator being in free fall within a gravitational field, and being at rest with no gravitational field present.  In his imagination, he experienced these situations, using his mind as a virtual lab.

But pure mathematicians, too, can experience new insights.  They often talk about stumbling upon a new way of understanding, a very experiential metaphor, like the expression "ah, now I see!"

From the moment we start studying mathematics, we need to experience the mathematical theory.  Unless we fall into a real experience of something that feels like a mathematical reality behind the symbols of theoretical constructs, we cannot know what theory means, and we cannot compare theory and experiment.

“three levels of insight”

In experimental physics, if you don't know how to operate the equipment, you cannot conduct experiments.  In theoretical physics, if you cannot understand the mathematics used in books and articles, you cannot engage in theory.  What is entailed in this understanding?  In my own experience, of experiencing theory, I have encountered three very different levels of insight.

The first level of understanding a mathematical theorem or derivation consists in following the written proof, step by step.  After checking that each next statement follows from the previous one, we can declare that we have checked the whole proof.  In other words, we then know that the proof is correct.  However, this kind of insight, while providing the practical value of certification (as long as we have been careful enough), does not provide much insight.

Algebraic step-by-step derivation

The second level of understanding, which often comes only after teaching the derivation to friends or students, is very different.  By the time we have thoroughly familiarized ourselves with the derivation, we can 'see' the whole derivation, all at once.  Let us take as an example the Pythagorean theorem. 

geometric direct-seeing illustration

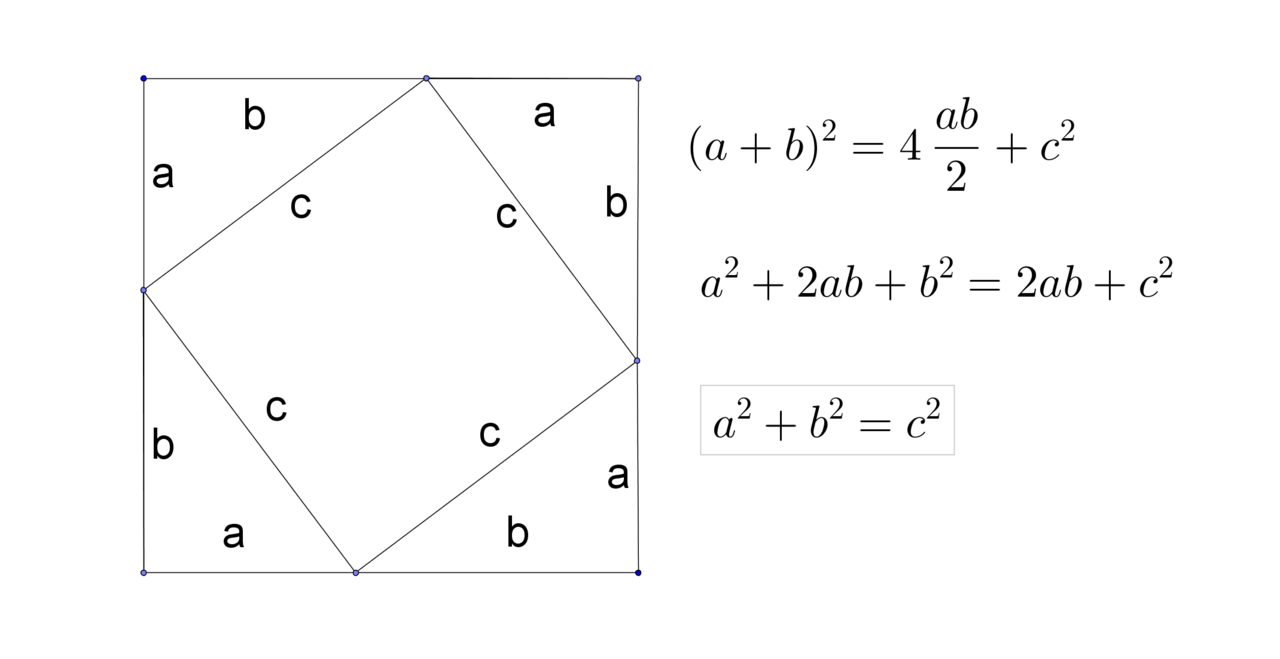
The upper figure presents a step-by-step algebraic derivation of the fact that the square of the hypotenuse c of a right triangle is equal to the sum of the squares of the other two sides, a and b.  Starting with the triangle at the top left, a seemingly unrelated calculation derives the square of the sum of the smaller sides, rather than the sum of the squares of the smaller sides.  But after a few steps of algebraic manipulation, the required result drops out, in a kind of magical way.

In contrast, the lower figure presents a geometric way of directly 'seeing the same result, after drawing a few extra lines and coloring some areas, without any further manipulation. The geometric derivation is equivalent to the algebraic derivation, as we can see from the fact that each other square in the lower figure has a surface area that is the square of the sum of the smaller sides: exactly the first step taken in the algebraic approach.  Still, the instantaneous seeing, in a kind of gestalt way, is what sets the second derivation apart.

This particular example does not contain many steps, and the fact that the first level uses algebra and the second one geometry is partly a coincidence.  For those deeply familiar with algebra, it is possible to 'see' even a lengthy algebraic derivation as a coherent unity that they can grasp (grok?) all at once.  And there are also geometric derivations that need to be constructed by a lengthy number of steps.

“going beyond”

The third level of understanding is yet again different.  After deriving a theorem step by step, first, and then 'seeing' the whole derivation as one coherent unity, we have become thoroughly familiar with it.  But what about the context of that derivation?  What if we change any of the assumptions?  What if we ask the same question in a different, richer space?  How to go about in setting up a new research program that aims at going beyond the theorem that we have just mastered on the second level?

What is needed at this point is an insight in how one could have discovered the theorem from scratch.  Imagine a state of the world in which the particular theorem we are studying had not yet been invented.  Can we 'see' how we could have stumbled on that theorem?  Can we imagine ourselves groping in the dark, exploring the 'space around' the particular theorem that had not been proved yet, perhaps not even formulated even as a hypothesis, and then hitting upon a derivation of that theorem?

It is that thorough familiarity, not only with the theorem, but with the context within which that theorem could have been discovered, that amounts to a third level of understanding. And once we reach that level, it may be possible to derive similar results, new and not yet seen before.

Piet Hut is President of YHouse (where this blog is hosted), Professor of Astrophysics and Head of the Program in Interdisciplinary Studies at the Institute for Advanced Study in Princeton, and a Principal Investigator and Councilor of the Earth-Life Science Institute in the Tokyo Institute of Technology.